ITエンジニアのキャリアに本気で向き合うメディア
ITエンジニアのキャリアに本気で向き合うメディア
目次
■キャリアとスキルアップ
2022.06.06 2024.06.28 約4分
今回は、『問題解決のための「アルゴリズム×数学」が基礎からしっかり身につく本』の著者 米田さんを招き、「30分でわかる！アルゴリズムの基本」をテーマに3つの問題を通してアルゴリズムの良さを紹介します。
キャリアの不安を解消しませんか？
キャリアにお悩みの方は、「Forkwell エージェント」をご活用ください！私たちが、無理に転職を勧めることはありません。エンジニアが転職のプレッシャーから解放され、自信を持って新たなキャリアを歩む手助けをお約束します。どの部分を強化し、どのように弱点を克服するのか、魅力的なポートフォリオの作成方法などをアドバイスいたします。
Forkwell エージェントに相談してみる（無料）
米田 優峻と申します。現在、東京大学2年生で AtCoder では E869120 で活動をしています。2021年12月に『問題解決のための「アルゴリズム×数学」が基礎からしっかり身につく本』という本を出版し、現在お陰様で2万部を超える販売部数となっております。「コンピュータは万能だ」 ― このようなイメージを持つ人もいると思いますが、実際はどんなに大量の計算処理も一瞬で行えるとは限りません。たとえば家庭用 PC の場合、60 個のモノの選び方を全部調べるだけで 100 年もかかってしまいます。そこで大切になるのは『アルゴリズム』すなわち計算の手順です。アルゴリズムを少し変えるだけで、100 年かかる計算が 1 秒に縮むこともよくあります。また、皆さんが便利に使っているカーナビや Google 検索などのツールにも、実はアルゴリズムが利用されています。本講演では、身近な例を用いてアルゴリズムの概観と面白さを紹介し、（アルゴリズムを）本格的に学ぶきっかけを作れたらと思います。また、アルゴリズムは数学とも密接に関わるので、中学～高校数学の広い範囲の中でどんな数学の知識が重要になるのかも取り上げます。
今回は「30分で分かる！ アルゴリズムの基本」というテーマで発表します。そもそもアルゴリズムとは何なのでしょうか？ 一言で表すと問題を解く手順、計算手順のことをアルゴリズムと呼びます。
まずは簡単な例として、1から100までの整数をすべて足す問題について考えてみましょう。要するに1+2+3+4…+100ということですね。
最も単純なのは1つずつ足していく方法です。100まで繰り返せば答えにたどり着くことは可能です。
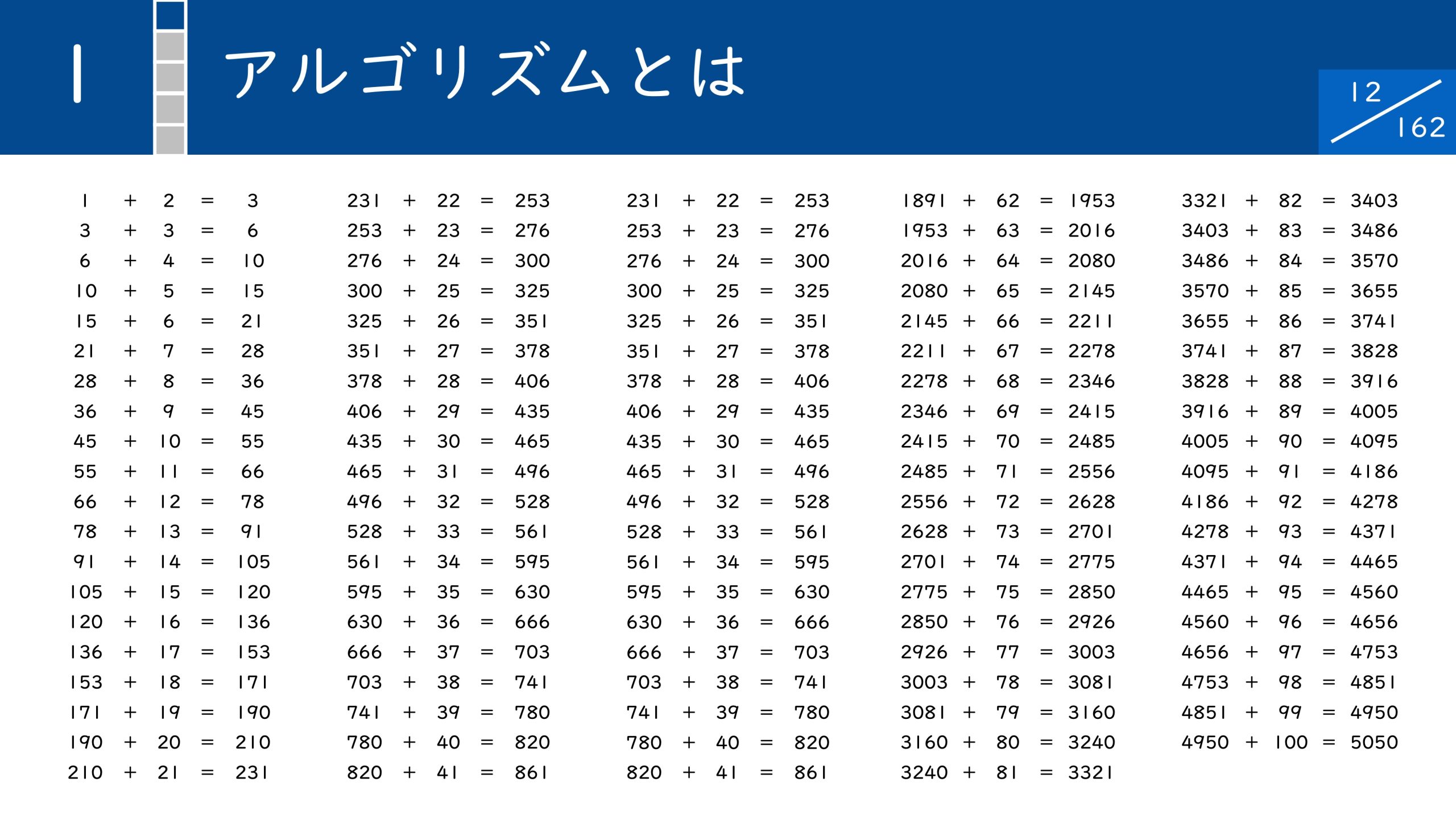
しかし、この方法では99回の計算を必要とします。この考え方だと計算が得意な人でも5分程度かかってしまうのではないでしょうか？
そこで考え方を変更し、合計が101となるペアを作ってみましょう。
全部で50個のペアが完成するので1〜100の合計が101×50であることが分かります。最初の手法では99回の計算を必要としていましたが、今回はたった1回の計算で答えを出すことができました。
先ほどもお伝えしたように、こうした計算の手順をアルゴリズムと呼びます。このアルゴリズムを少し改善するだけで計算が劇的に速くなることがあります。先ほども99回の計算が1回になりましたが、アルゴリズムの威力はさらに強力で、2週間かかる問題が0.01秒になることもあります。
本講演では以下の3つの問題を通して、アルゴリズムの威力についてお伝えします。
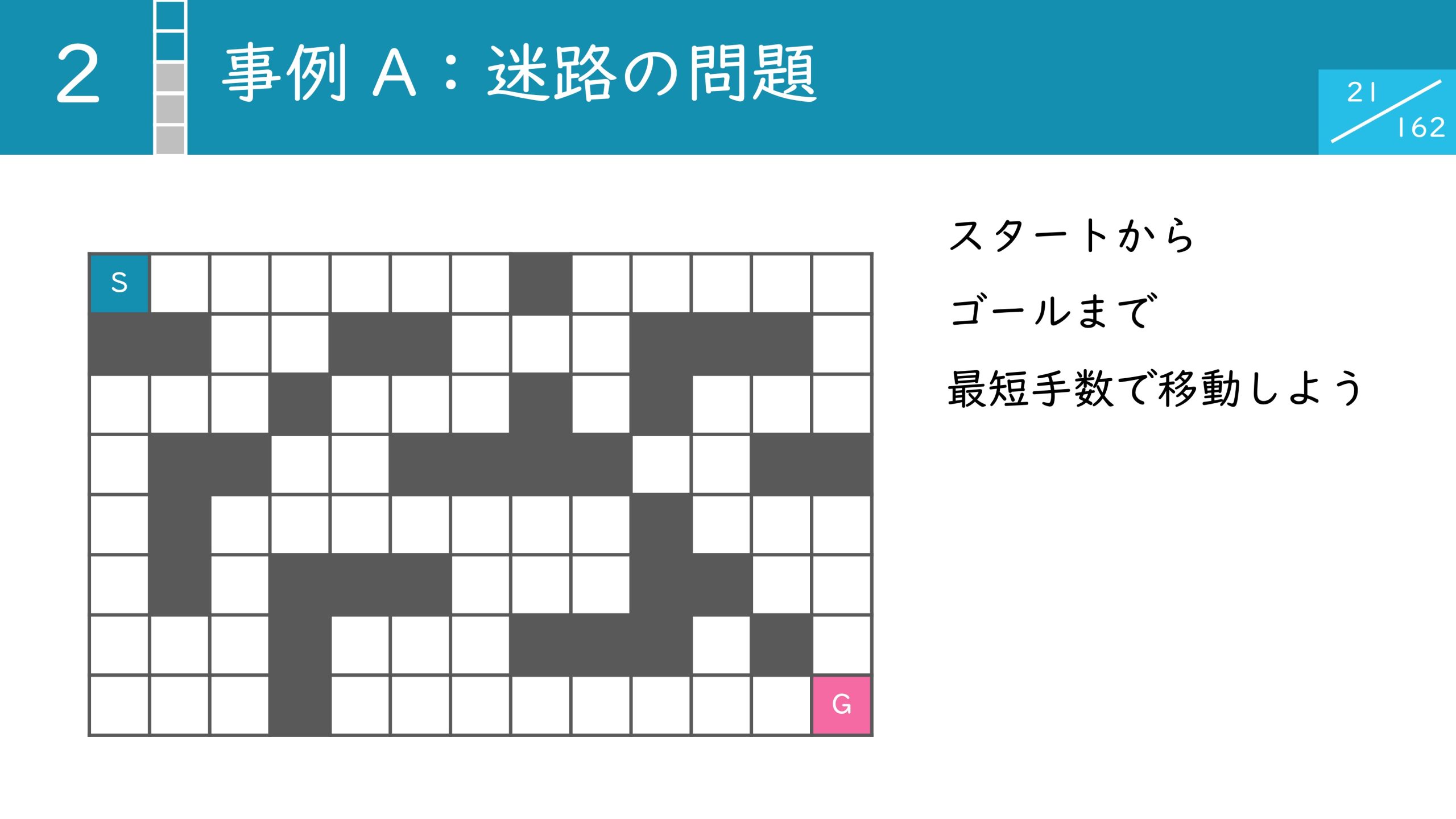
Twitterで話題になったので、ご存知の方もいらっしゃるかもしれません（笑）「スタートからゴールまで最短手数で移動しよう」という迷路の問題です。
ルールはシンプルで、1手で上下左右の隣接するマスに移動することが可能です。では、何手が最短なのか？最短ルートはどの様なルートなのか？を考えてみましょう。
皆さんはどのようなルートを思いついたでしょうか。直感的に思いつくルートはいくつかあるものの、それを正解だと確信するのは難しいと思います。
もちろん、すべてのルートを検証すると、答えを求めることができます。しかし、この迷路はルートが全部で216通りあり、すべて調べるのはかなり辛い作業になります。そこでアルゴリズムを変えてみましょう。
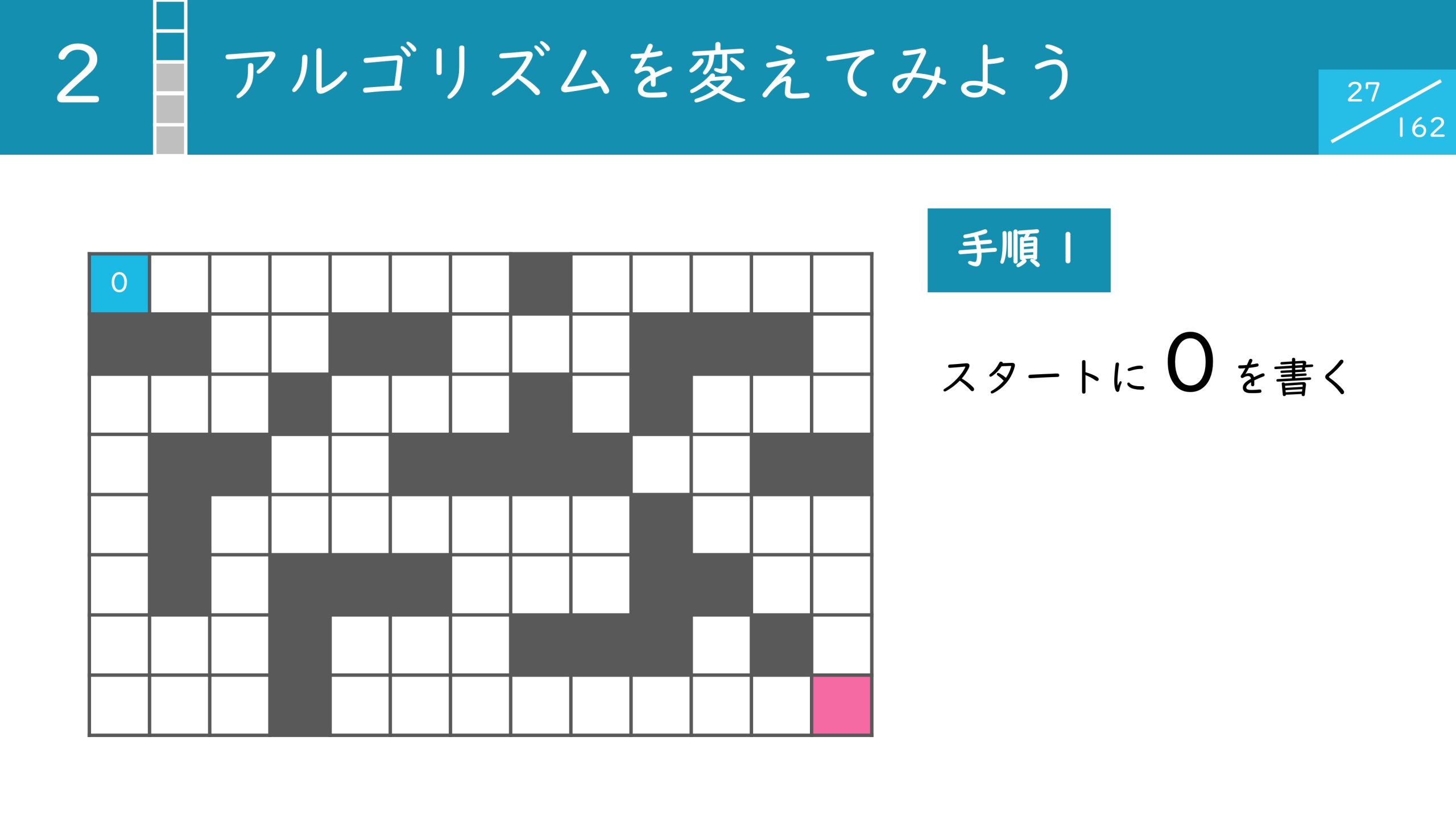
まず、スタート地点に0を記入します。その後、隣接するマスに1を書き込みます。さらにその隣に2を記入し、同様に3と記入していきます。4まで記入するとこの図の様になります。
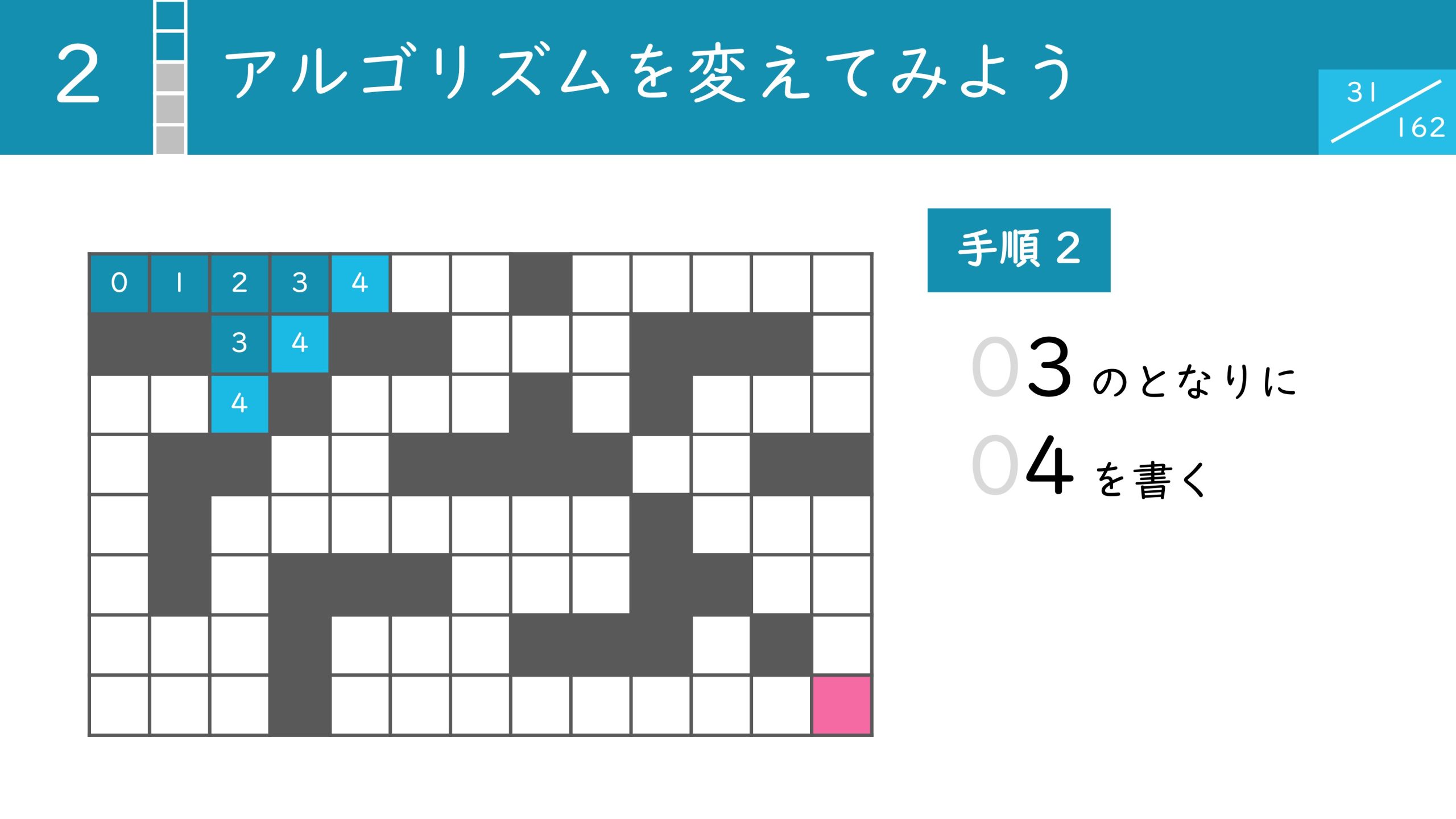
それぞれのマスに記入されている数字はそのマスまでの最短距離を表しています。この作業を繰り返していくと
最終的にすべてのマスが埋まりました。ゴールのマスには23と書かれています。マスに書かれている数字はそのマスまでの最短手数を表しているので最短手数が23手であることが分かりました。
また最短手数のルートはゴールから出発し、数字の減る方向に移動することで導けます。
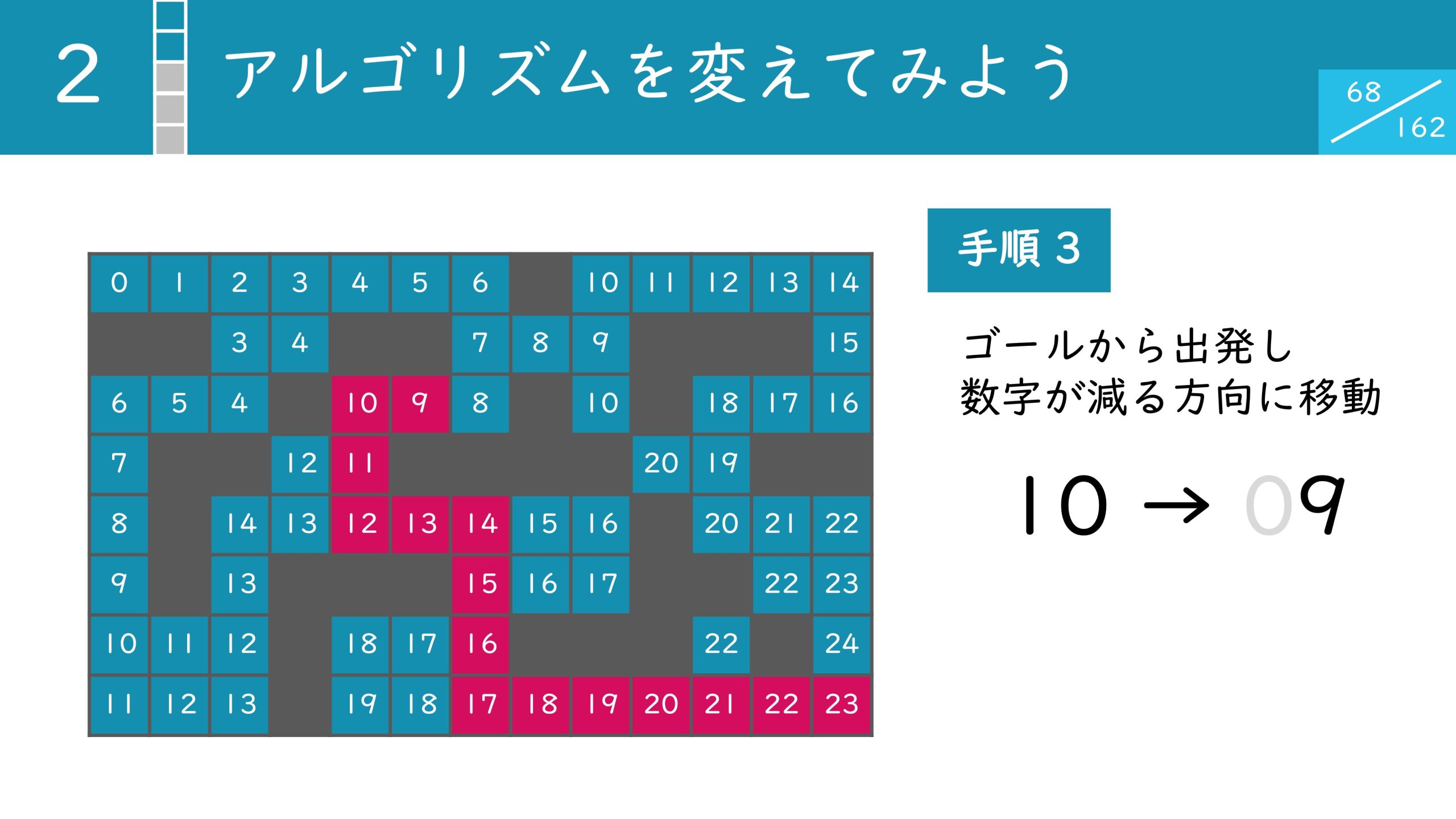
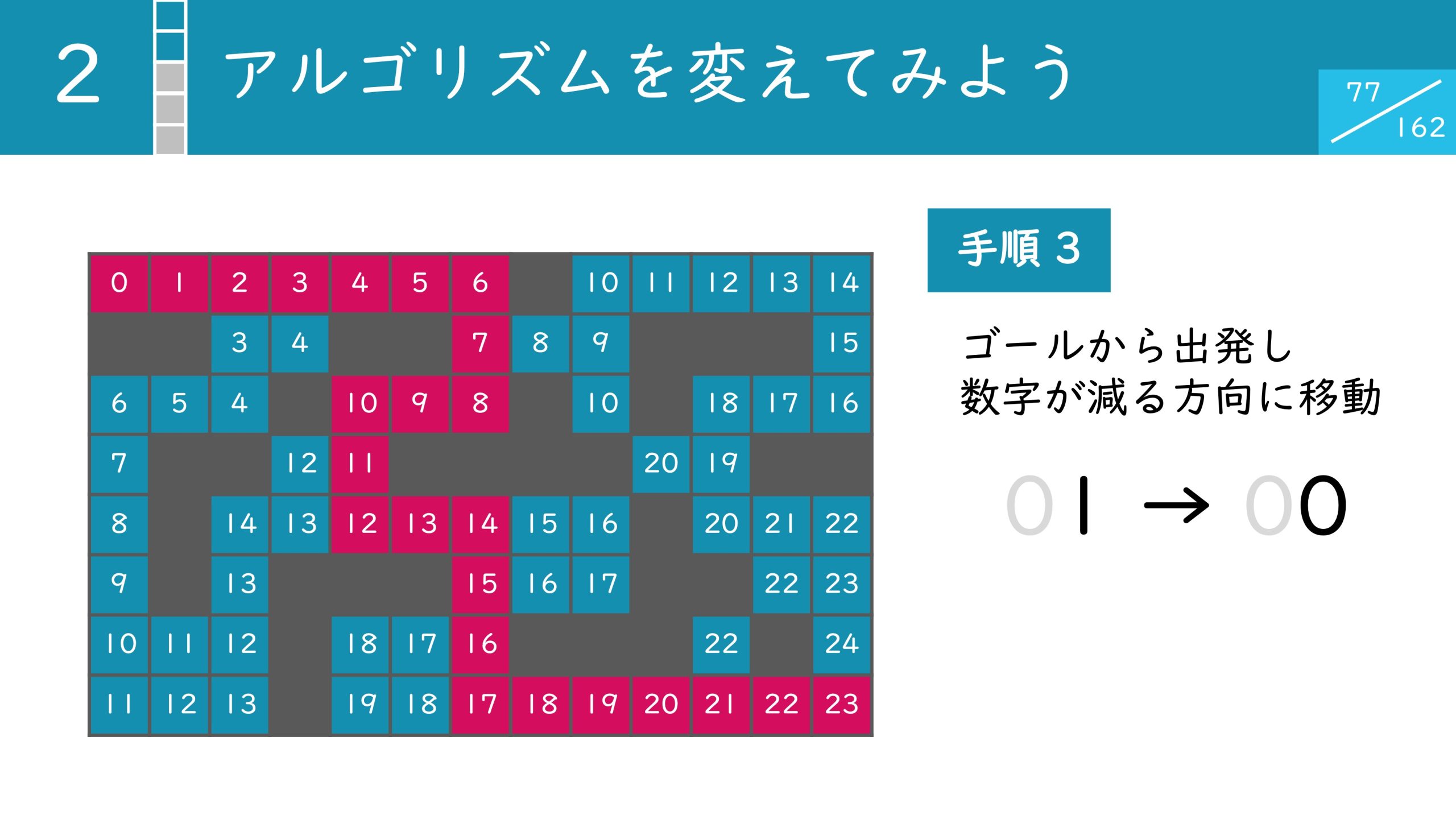
23手で実際に移動できるルートを求めることができました。この一連のアルゴリズムを幅優先探索と呼びます。単純な解法では216通りも調べる必要がありましたが、アルゴリズムを改善するだけで、手計算で簡単に求められるレベルになりました。
次の事例はプログラムのデバッグです。皆様もプログラムを書いていれば当然バグが発生しますよね。
例えば100行のプログラムの中に1つのバグがあるとします。途中にバグがあればその後の計算も合わないので、バグ地点以降は正常に動作しないものとして仮定します。そこで、皆様ならどのようにバグを見つけますでしょうか。
もちろん、「1行目は正常に動作しますか？」「2行目は正常に動作しますか？」といったように、すべての行をチェックすることで、バグを見つけられますが、最悪の場合、100行すべてを確認することになります。
100行程度であれば可能かもしれませんが、実務の中では1万行や10万行を超えるプログラムを書くこともありますよね？
1つずつ確認していくのは現実的ではないので、少ない手順でバグの所在を突き止める方法を考えてみましょう。
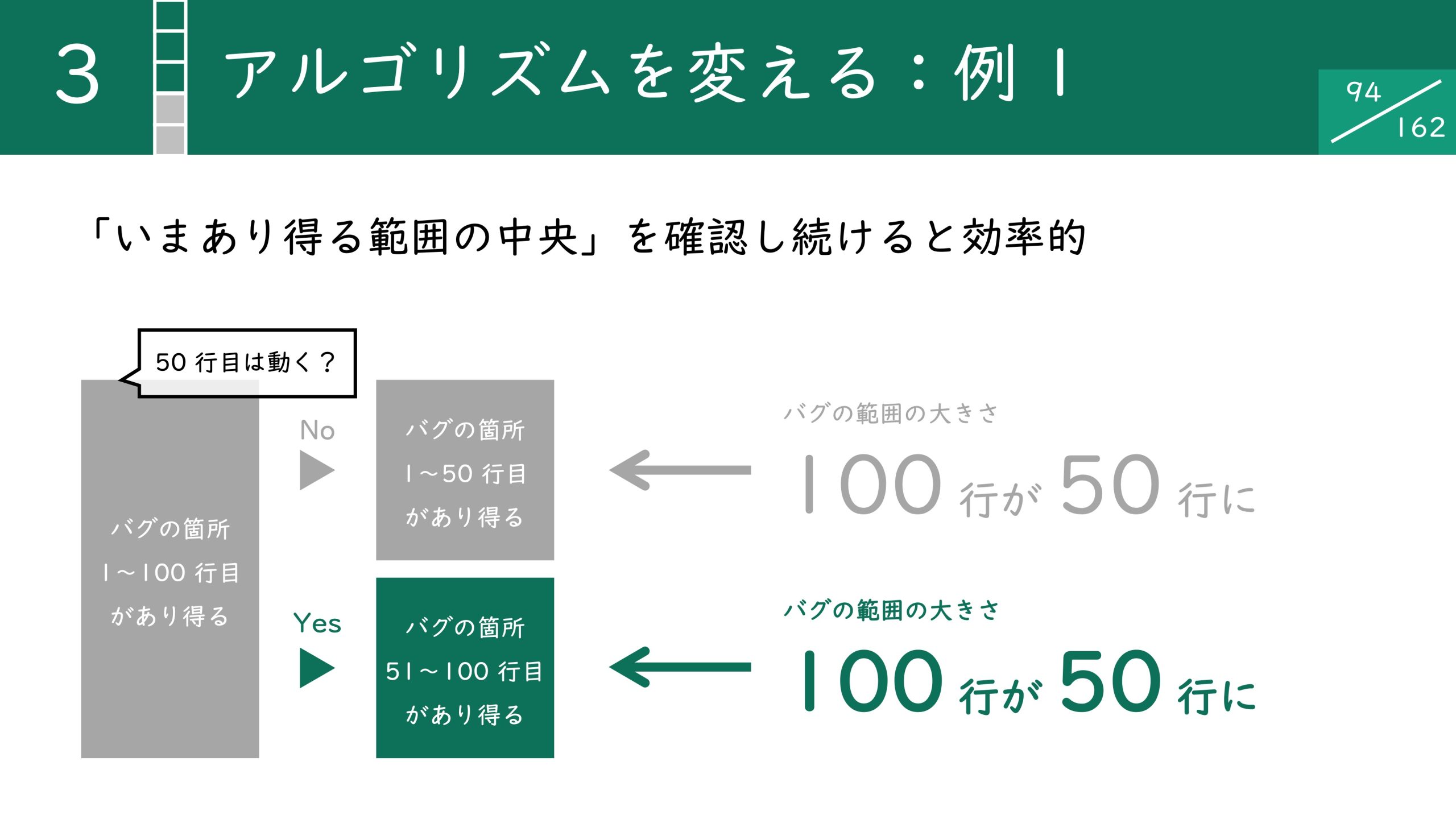
実は「今あり得る範囲の中央」を確認し続けると効率的です。何もチェックしていない最初の段階ではバグは1行目かもしれないし、77行目かもしれません。つまり1行目から100行目まですべてにバグの可能性がある状態です。
これに対して1〜100の中央となる50行目を確認します。これで仮に50行目が動かない場合、バグの所在が1〜50行目に絞られます。逆に50行目が正常に動作する場合、51行目から100行目にバグがあることが分かります。1回の確認で範囲を半分に絞り込むことができました。
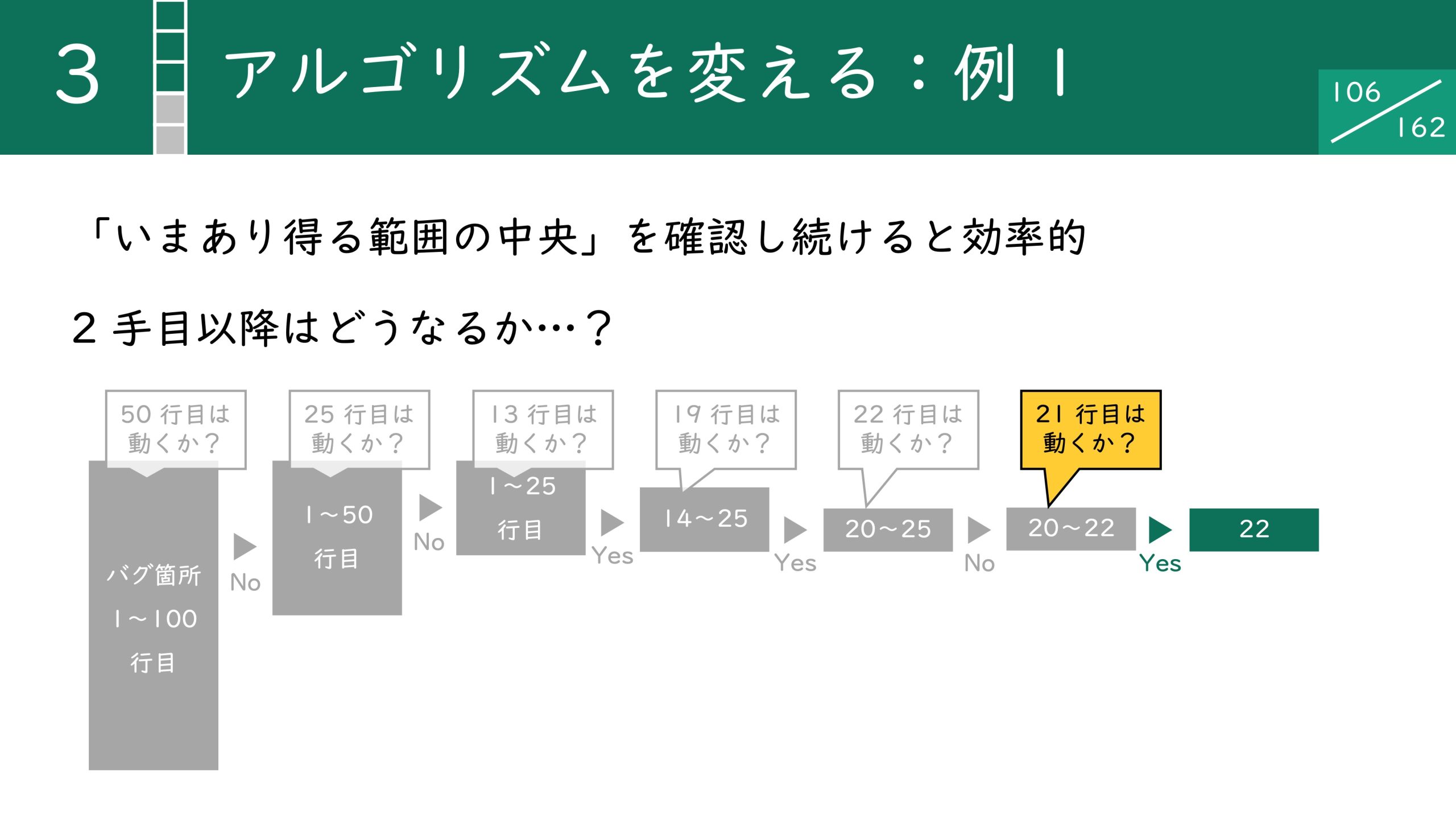
最初の確認で50行目が動かなかった場合、1〜50行目にバグがあることになります。2手目は1手目と同様に、中央である25行目が動くかを確認します。動作しない場合は1行目から25行目に絞ることができます。
次も同様の手順で13行目を確認し、Yes の場合は14〜25行目に範囲を絞ることができます。次も同様の手順で19行目を確認し、No の場合は 20～25 行目に範囲を絞ることができます。ここまで4回の確認作業しかおこなっていませんが、すでに100行から20〜25行の6行にまで絞り込めています。
次は22行目を確認します。これが No の場合は20行目〜22行目まで絞り込めます。同様に21行目が動くかを確認し、Yes の場合は22行目にバグがあることが分かりました。なんと6回の確認作業でバグのある行を発見できています。これは果たして偶然でしょうか？
今度はバグが77行目にあった場合を考えてみましょう。
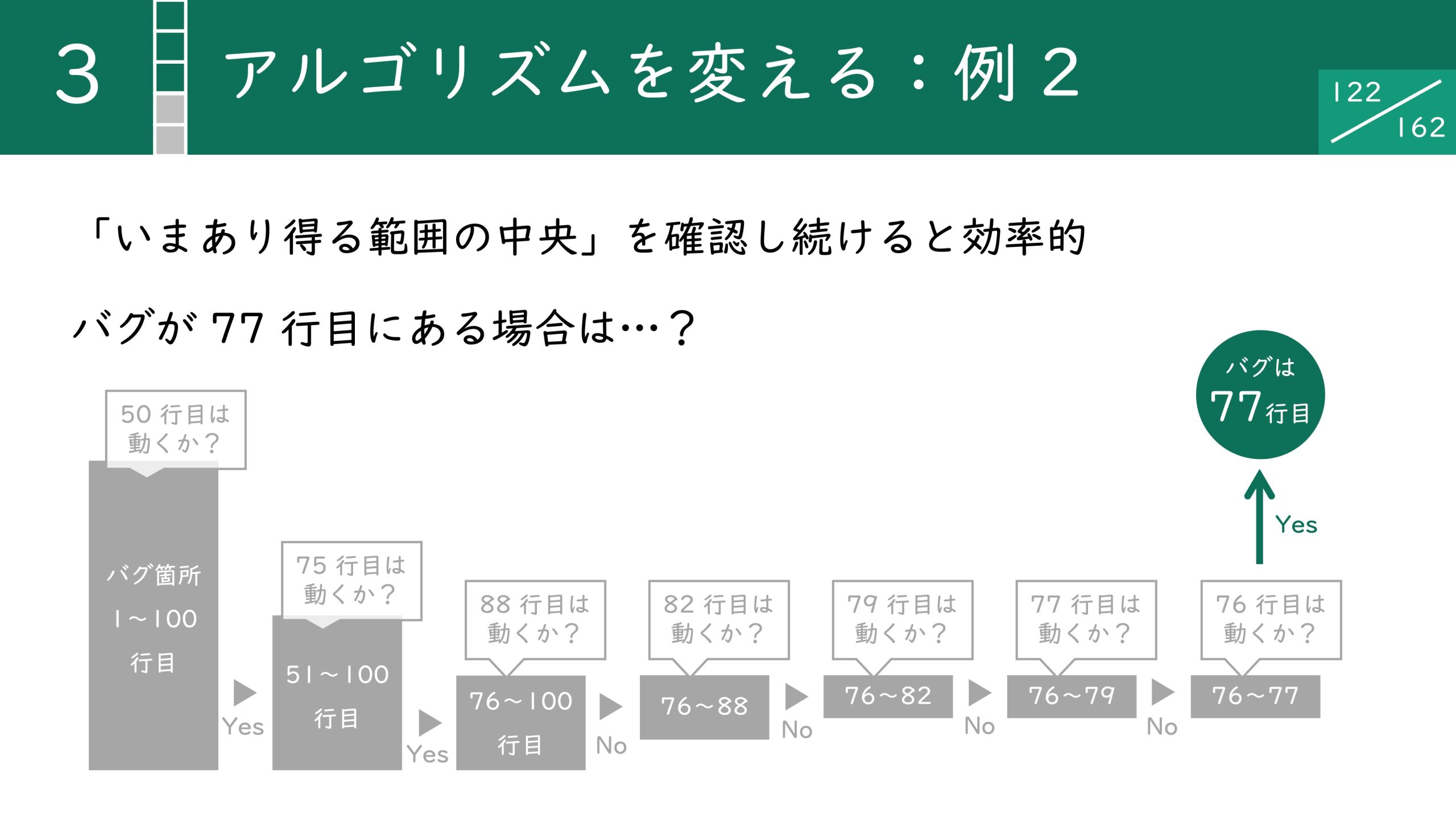
前回より手数が増えましたが、7手でバグを突き止めることができました。果たしてこの方法では最大、何手かかるのでしょうか？
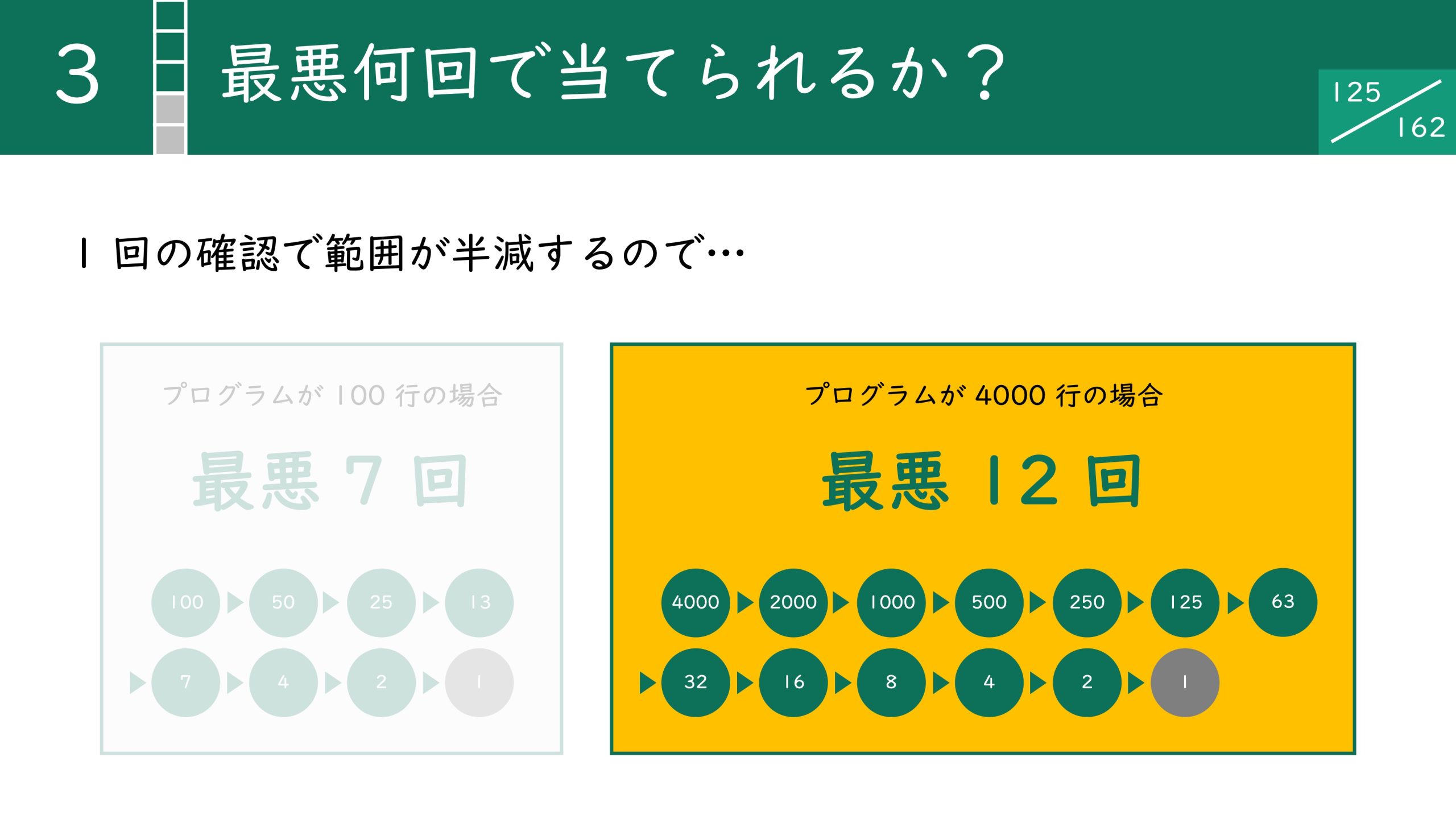
100行のプログラムの場合は最大で7手かかります。1回の確認で探索範囲が半減するので100の半分は50、50の半分は25と計算していくと7回で1にたどり着くことができます。
100行で7回といっても大したことではないように思えるかもしれませんが、、4,000行にしても12回の計算で答えを導き出すことができます。仮に10億行でもなんと30回で特定できます。この一連のアルゴリズムを二分探索法と呼びます。
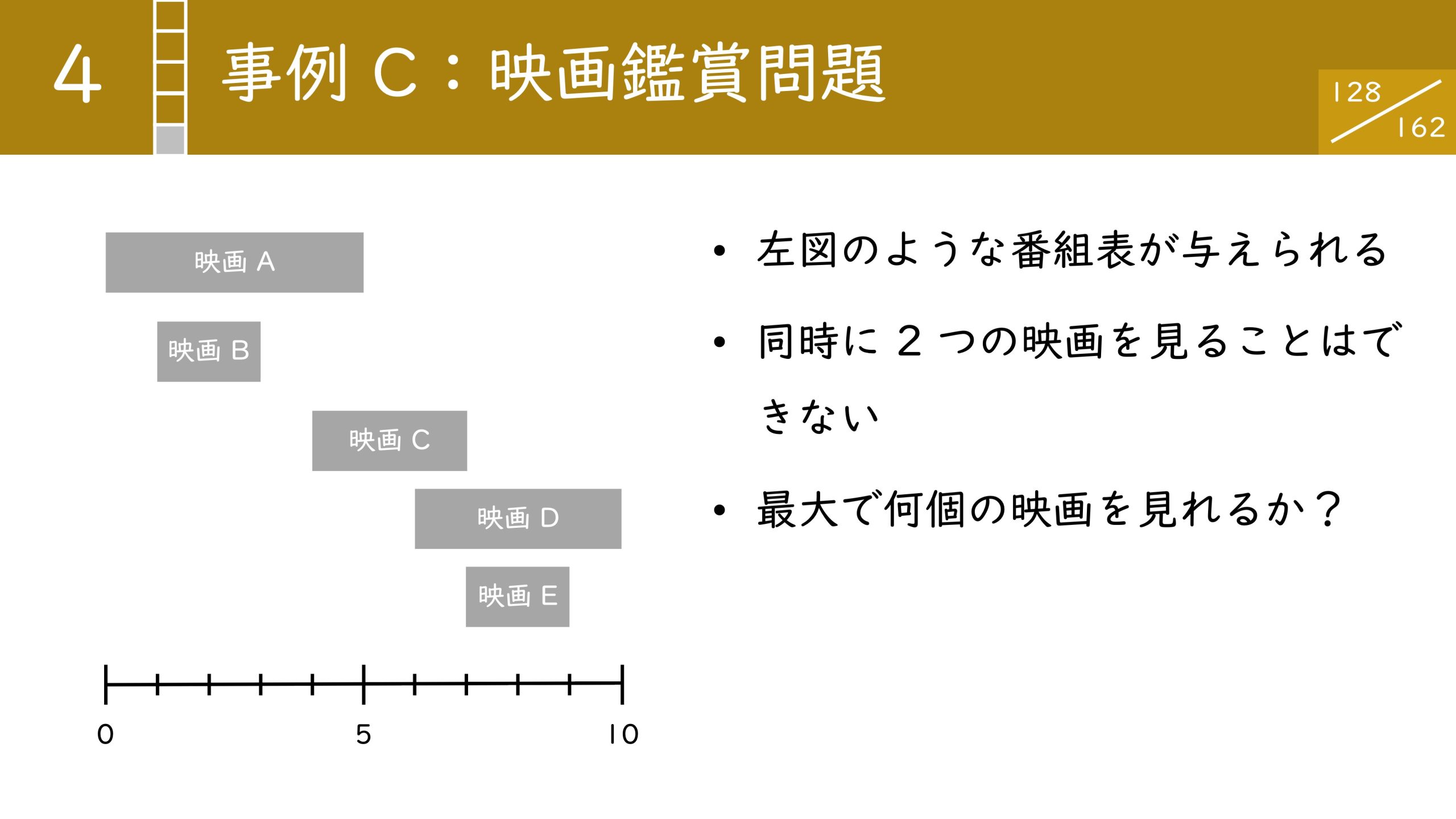
最後の事例は映画鑑賞問題です。
映画Aの時刻が0時から5時まで、Bが1時から3時まで、Cが4時から7時というように上映時間が決まっています。この中でできる限り多くの映画を見るにはどうすればよいか？を考える問題です。
2窓はできません。たとえばAとCは時間が重複しているので両方選ぶことはできません。
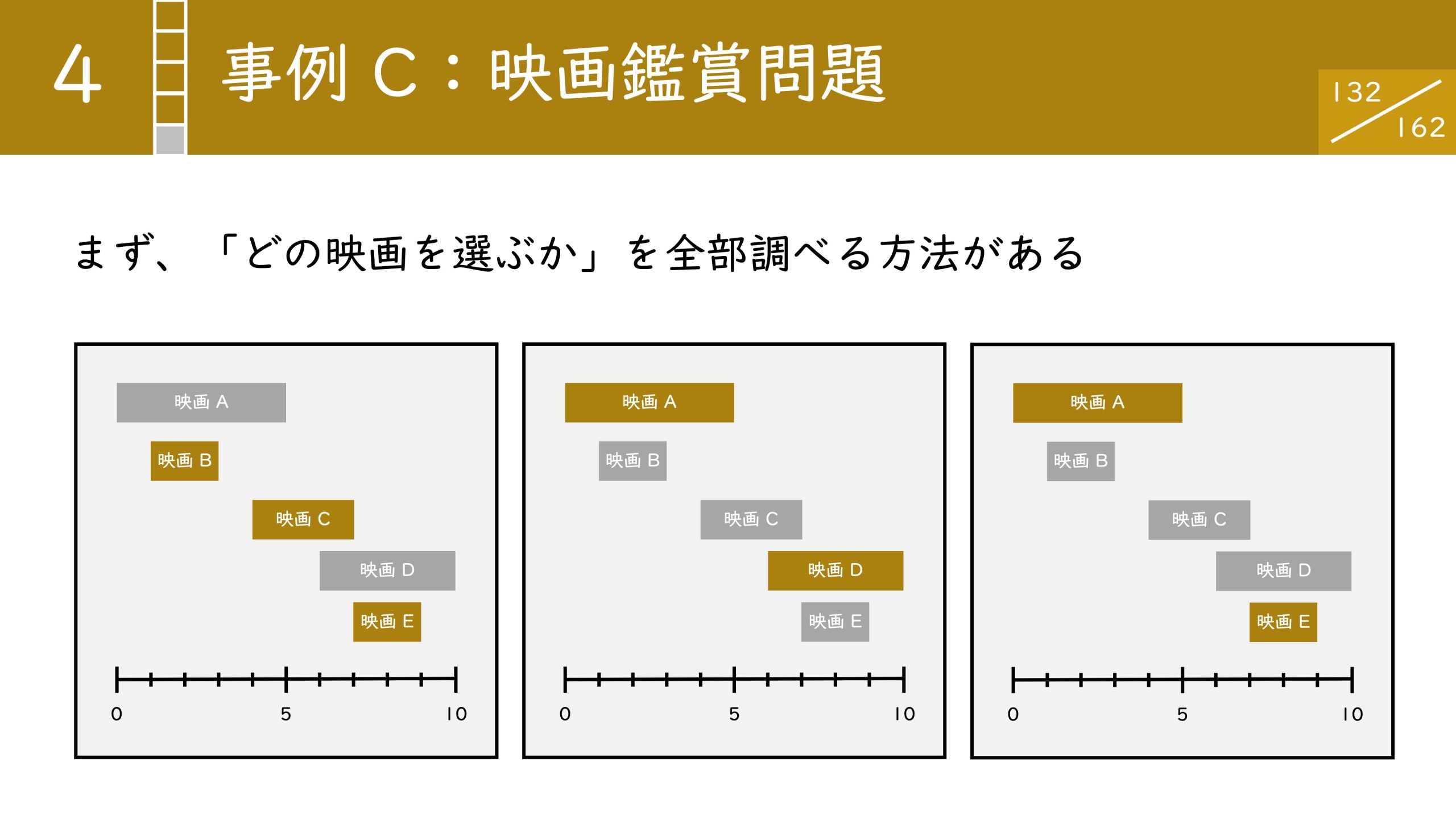
答えは 3 つです。映画 B と C と E を選べば、最大で 3 つの映画を見ることができます。
それでは、どうやって最適解を求めるのでしょうか。これまでの問題と同様、「あり得る映画の選び方」をすべて調べれば、最適解にたどり着くことができます。
たとえばスライドの例では映画が 5 本ですので、以下のような選び方を調べる必要があります（もちろんそれ以外にもあります）。
そこで、映画が 50 本の場合は何通りの選び方を調べる必要があるのでしょうか？いきなり50本の映画から考えるのは大変なので小さく始めてみましょう。
映画が1本しかない場合は「（見ることを）選ぶ」「選ばない」の2通りになります。
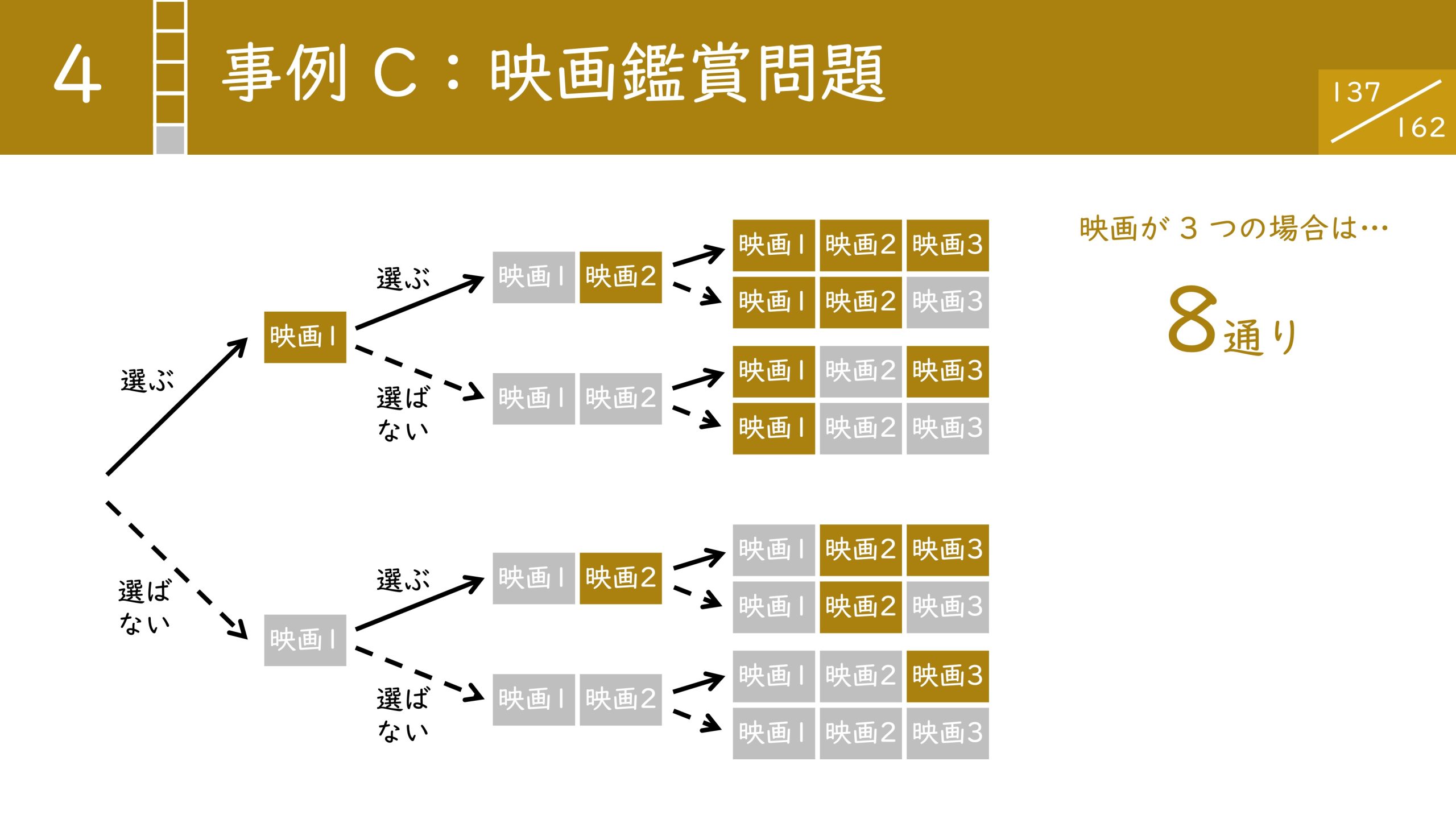
3本まで来ると8通りまでパターンが増えます。1本のときは2通り、2本なら4通り、3本なら8通りと倍々でパターンが増えてきました。
では果たして、50本までいくとどうなるでしょうか？
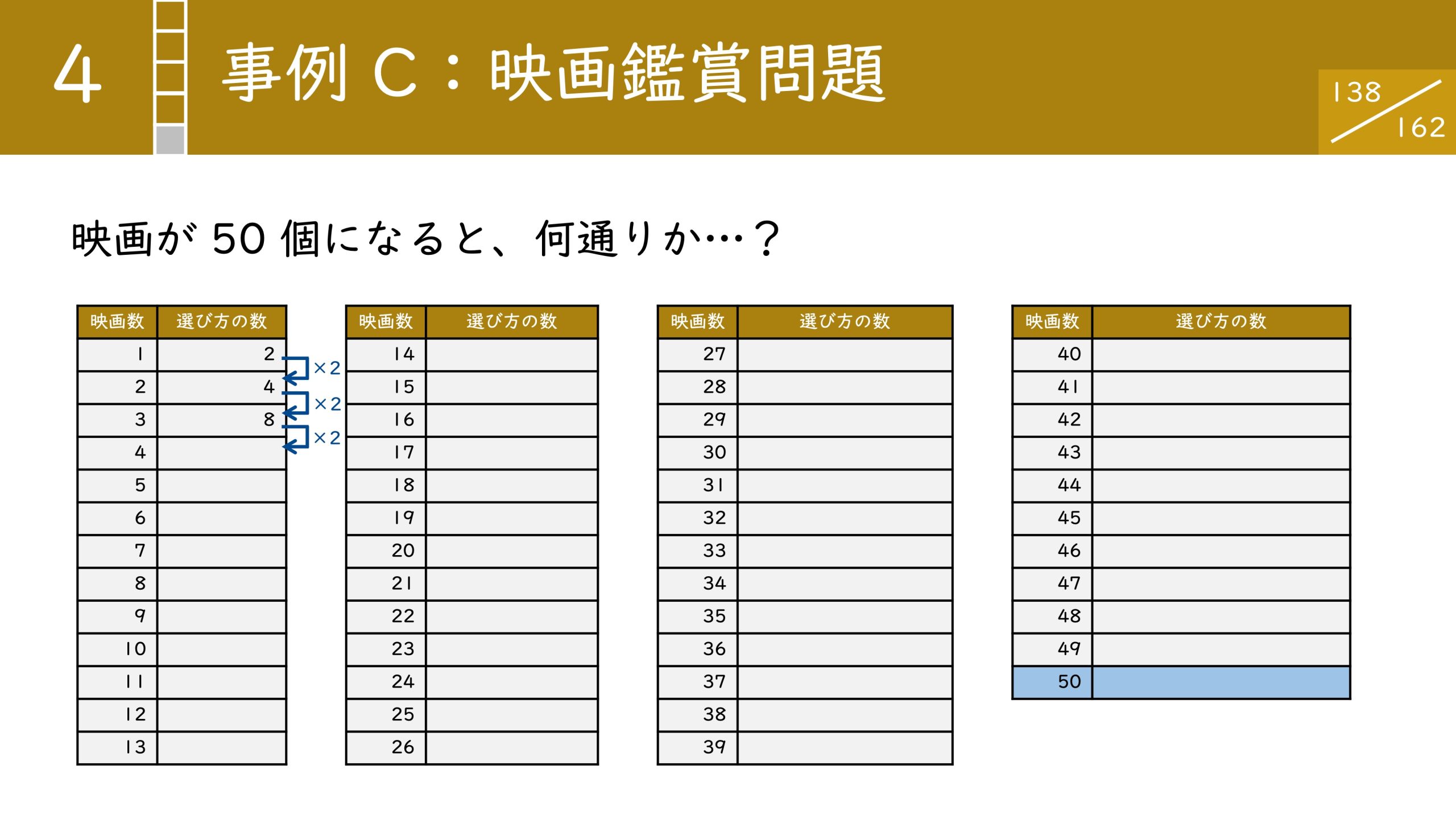
全部で1,125兆通りのパターンがあります。ここまで来ると手計算は不可能ですね。
とはいえ、皆様の中には現代のコンピューターさえあれば1,000兆通りのパターンでも容易に計算が可能なのではないか？と考える方もいるかもしれません。
しかし、残念ながらそれは正しくありません。
一般的な家庭用パソコンではおよそ1秒に10億通りを探索できるといわれています。単純計算で1,125兆を10億/秒で割ると約110万秒であり、約2週間です。映画50本程度でも、すべてのパターンを調べると2週間かかってしまいます。
当然ですが、2週間も待つことはできません。そもそも人気のない映画だと、公開から2週間ぐらいで劇場から消えます。
「最適な映画の組み合わせを考えていたら、見たい映画の上映が終わっていた」という悲劇に見舞われないために我々はどうしたらよいのでしょうか？
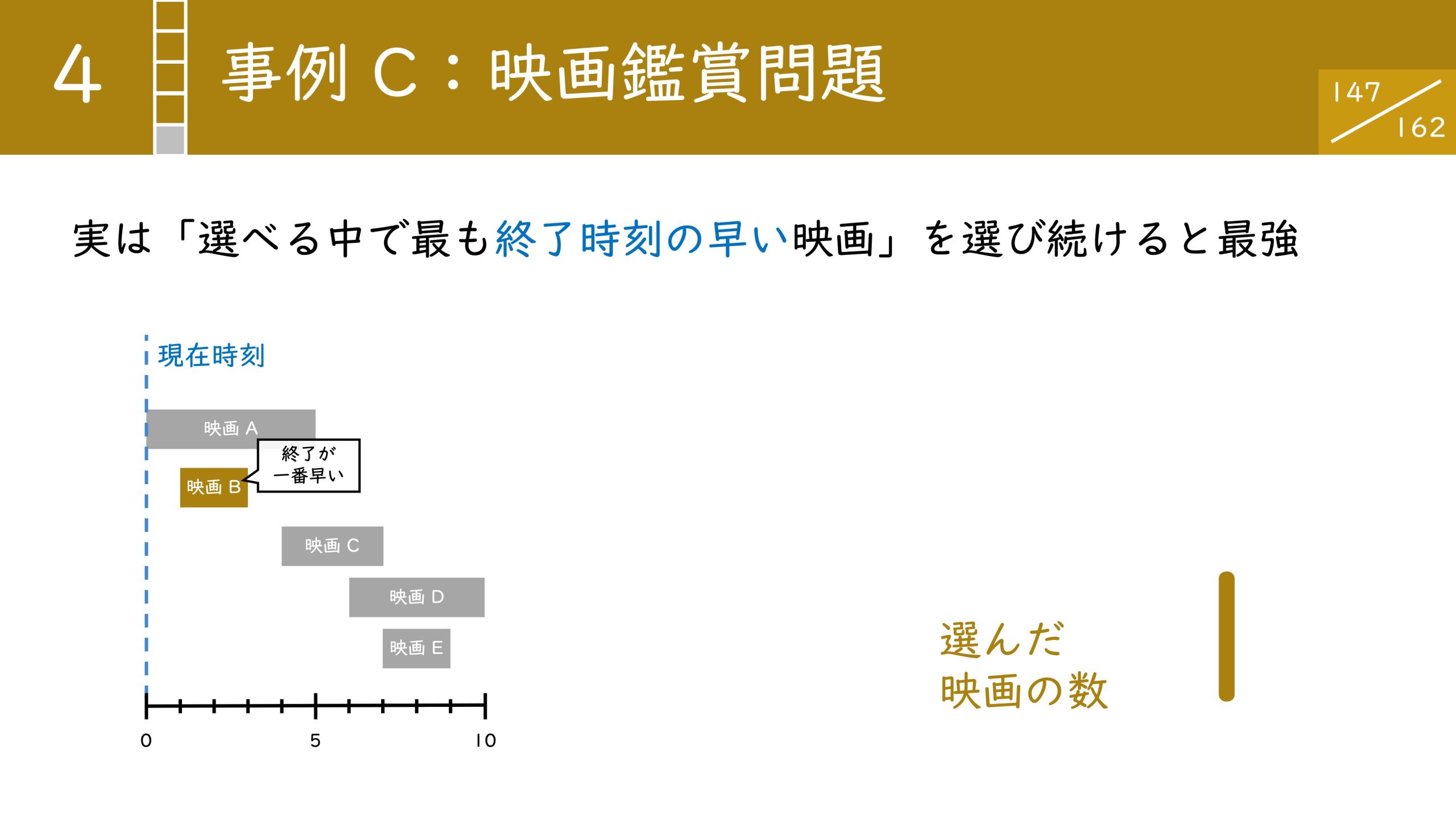
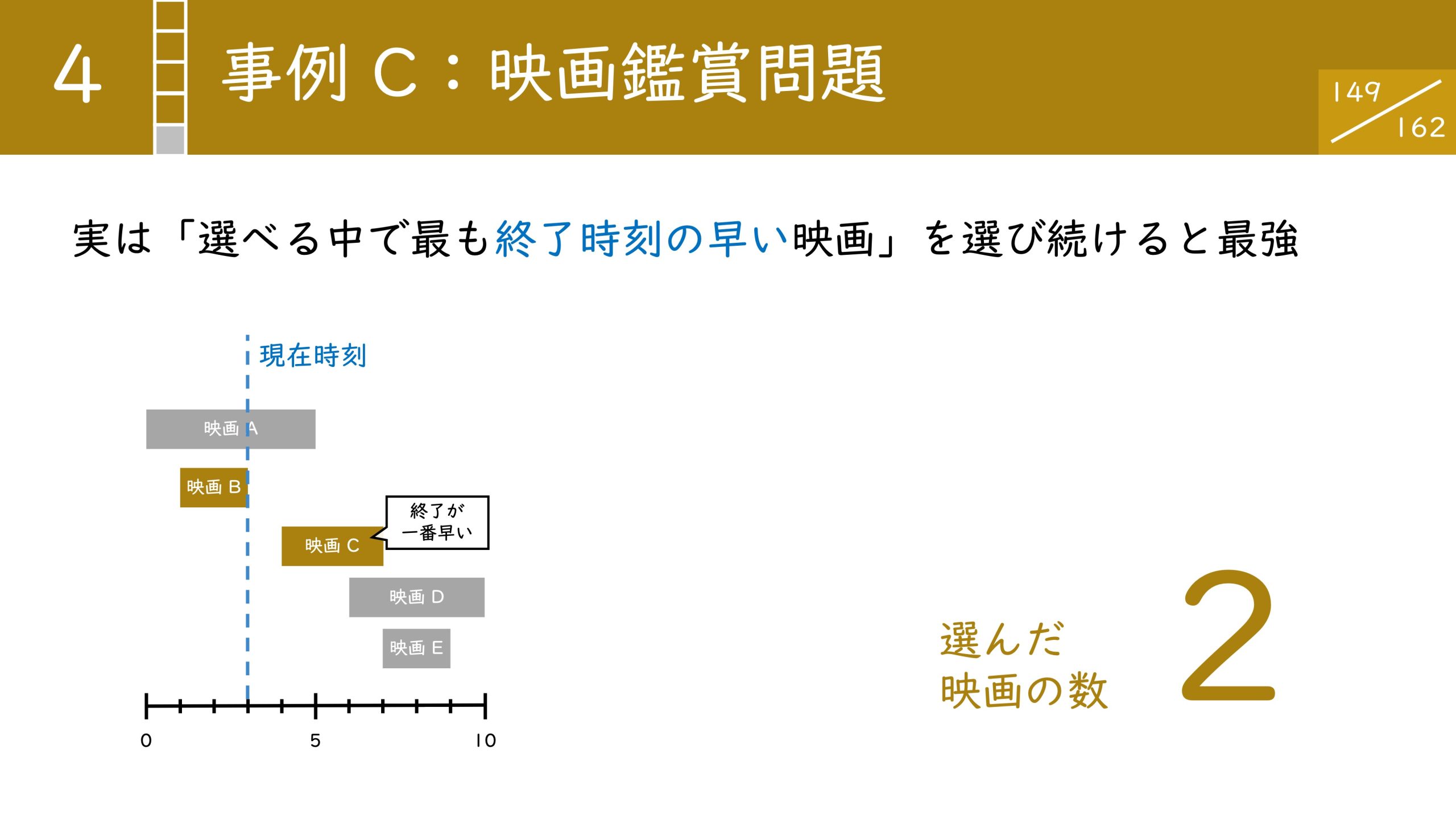
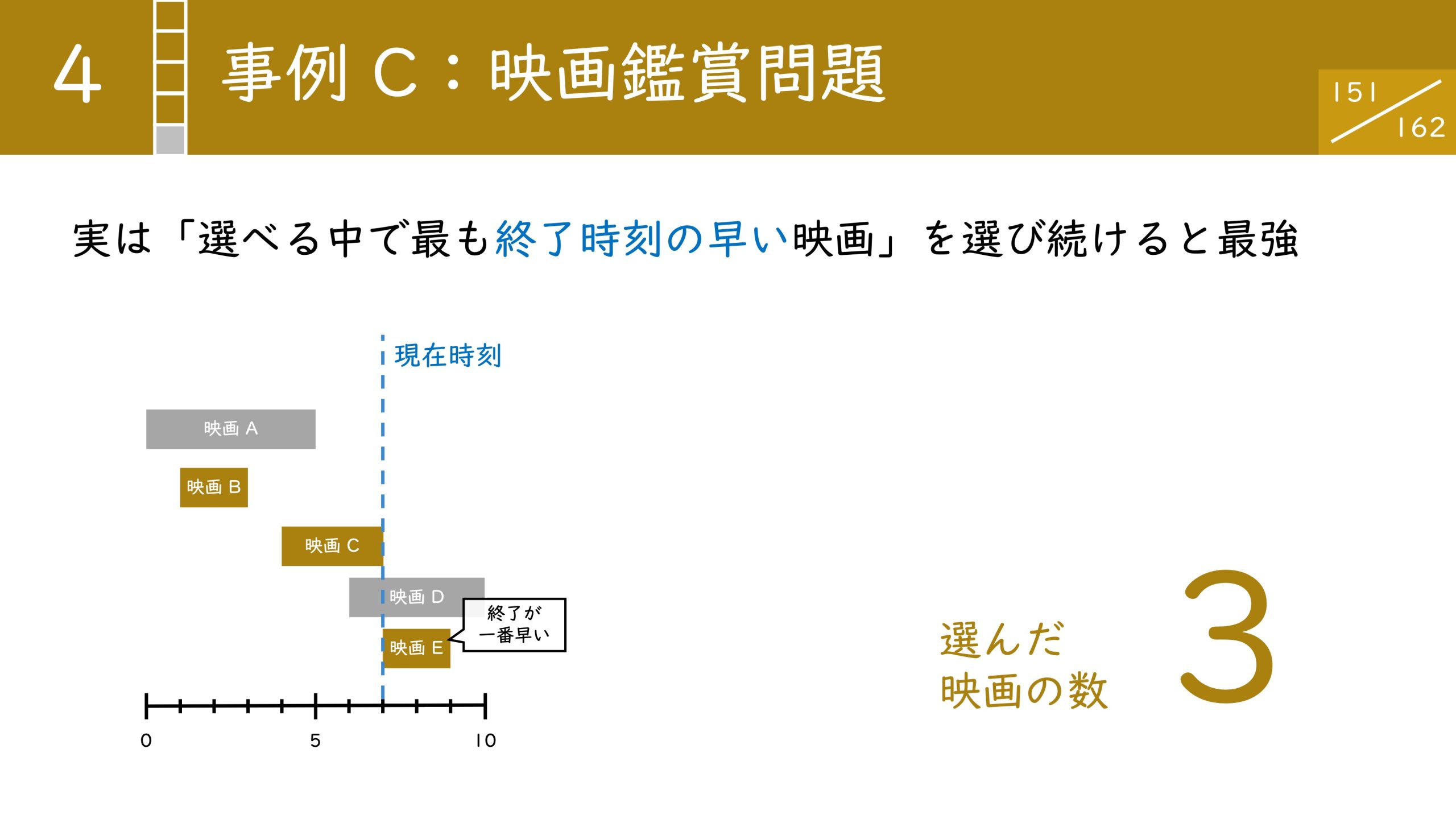
実は、選べる中で最も終了時刻の早い映画を選び続けると、最適解が得られます。具体的な流れは以下のようになります。
すると最終的に映画BCEの3本を見ることができました。最初に示した通りの最適解にたどり着くことができています。もちろん偶然ではなくアルゴリズムとして成立している手法です。
この手法を使うことでどれほどの効果があるのでしょうか?
たとえばコンピュータを使って計算した場合、この手法を使うと映画が50本でも0.01秒以内に答えが分かります。多少面倒ですが仮に手計算をしたとしても、タイムスケジュールのような図があれば10分程度で答えを導くことができるでしょう。
2週間が0.01秒になる。これがアルゴリズムの力です。
計算の手順＝アルゴリズム
というお話をしました。他にも問題を解く手順、問題解決手段といってもいいでしょう。
さて、皆様の中には、日頃から様々な計算をコンピュータに委ねている人が多いのではないのでしょうか。そんなコンピュータも万能ではなく、時間がかかる問題に直面することもあります。
しかし、アルゴリズムを見直すことで2週間かかる問題を0.01秒で解くことができます。このアルゴリズムの力強さが皆様に伝わっていればうれしいです。
今回は以下3つの問題を通じてアルゴリズムの良さを紹介しました。
今回紹介した例以外にも実社会でアルゴリズムが活用されている例はたくさんあります。例えば皆様おなじみの順位表作成（ソート）を始め、乗換案内やカーナビなどにもアルゴリズムが活用されています。
アルゴリズムは便利ですが、学ぶためには数学も必要です。例えば計算回数を考えるとき、指数関数や対数関数などの知識が求められることもあります。
デバッグ問題の例では、二分探索法の説明をしましたが、プログラムの行数をnとすると二分探索法の回数は最悪ケースで log n 回になり、対数関数が出てきます。この他にもさまざまな数学的知識が求められるケースがあります。
しかし、それ以上に重要なのが数学的思考力だと考えます。
アルゴリズムと数学が同時に学べる新しい入門書がありますのでせひ皆で学びましょう！
上記の特徴がありますので、アルゴリズムに興味のある方はぜひ手に取っていただければ幸いです。
転職は思ったよりも、時間がかかる
年収800万円以上のハイキャリアでも、42%が転職に1年以上かかっています。
技術力が高いほど、転職先が限定される
スキルや志向が明確なほど、マッチするポジションは限定されます。
ハイキャリアでも、面接には落ちる
素晴らしいキャリアでも面接に落ちることは珍しくありません。メンタル対策や面接の振り返りをサポートします。
自分のペースで進めたいなら「スカウトをON」
エージェントに頼らずスカウトメールから直接応募も可能です。
Forkwellエージェントは、企業選びから面接対策まで、あなたの転職活動を徹底的にサポートします。「経験チャート」機能を利用すれば、たった3分であなたの経歴を作成できます。
『問題解決のための「アルゴリズム×数学」が基礎からしっかり身につく本』著者 2002年生まれ。2021年、筑波大学附属駒場高等学校を卒業し、現在は東京大学1年生。競技プログラミングではE869120というハンドルネームで活躍。2020年までに国際情報オリンピック（IOI）で金メダルを三度獲得。また、アルゴリズム関連の研究でも日本学生科学賞・MATHコンなどで数々の実績を残している。その他、Qiitaで多数記事を投稿するなど、アルゴリズムや競技プログラミングの普及活動にも取り組んでいる。著書『「アルゴリズム×数学」が基礎からしっかり身につく本』は5刷2万部。
